反向传播(BP)算法的推导
神经网络优化任务的一般描述
一个估计器可以描述为如下形式. 其中\(\mathbf \Theta\)是参数集合, \(\mathbf x\)和\(\mathbf{\hat y}\)分别是输入和输出.
\[\mathbf{\hat y} = f(\mathbf x, \mathbf \Theta)\]而学习目标则要求最小化损失函数\(J\)
\[\min_{\mathbf \Theta} J(\mathbf \Theta, \mathbf x, \mathbf y)\]如果\(J\)是比较简单的形式, 如感知机中的均方误差MSE, 那么可以将\(J\)视为\(\theta\)的函数, 直接求导后使用梯度下降进行最优化求解. 下式中的\(\lambda\)为学习率.
\[\theta \leftarrow \theta - \lambda \nabla_\theta J(\theta), \quad \forall \theta \in \mathbf \Theta\]为方便理解, 可以将\(\theta\)视为自变量, 而\(\mathbf x\)和\(\mathbf y\)视为损失函数的参数.
但是如果\(J\)是比较复杂的形式, 比如是某个\(\theta \in \Theta\)的复合函数, 甚至对每个参数\(\theta\)的复合层级并不一致, 那么无法直接求得\(J\)对\(\theta\)的偏导数. 多层神经网络就是一个例子. 在这种情况下, 就需要用到反向传播(BP)算法.
BP算法一般形式的推导
首先回忆一下复合函数求导法则和多元复合函数求导法则:
\[\begin{align} \nabla_x f\bigl(g(x)\bigl) & = \frac{\partial f}{\partial g} \frac{\partial g}{\partial x}\\ \nabla_x f\bigl(g(x), h(x)\bigl) & = \frac{\partial f}{\partial g} \frac{\partial g}{\partial x} + \frac{\partial f}{\partial h} \frac{\partial h}{\partial x} \end{align}\]考虑如下图所示的神经元, 其中一个神经元的输出被多个不同分支的神经元作为输入(当然也可以是一个或者没有).
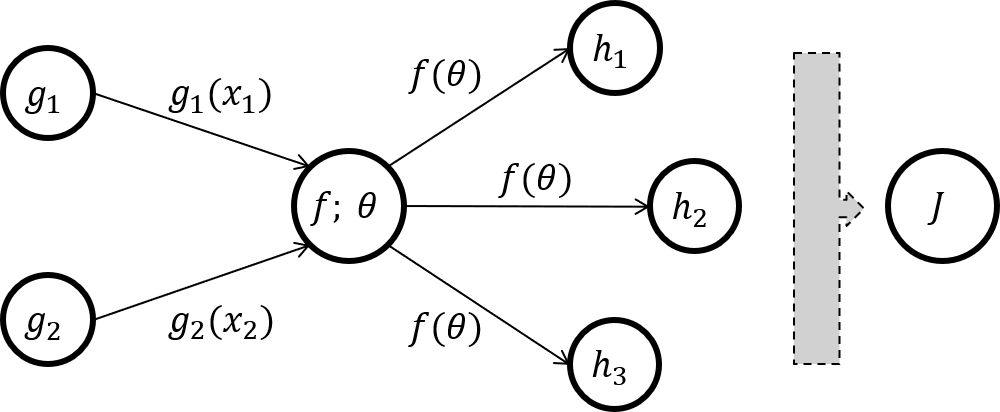
这里的损失函数可以表示为\(f, \mathbf h\)的多元复合函数
\[J(\theta) = J\Bigl(h_1\bigl(f(\theta)\bigl), h_2\bigl(f(\theta)\bigl), h_3\bigl(f(\theta)\bigl)\Bigl) = J\Bigl(\mathbf h \bigl(f(\theta)\bigl)\Bigl)\]那么损失函数对参数\(\theta\)的偏导数呼之欲出
\[\begin{align} \nabla_f J & = \frac{\partial J}{\partial h_1} \frac{\partial h_1}{\partial f} + \frac{\partial J}{\partial h_2} \frac{\partial h_2}{\partial f} + \frac{\partial J}{\partial h_3} \frac{\partial h_3}{\partial f} = \nabla_{\mathbf h} J \cdot \nabla_f \mathbf h\\ \nabla_\theta J & = \frac{\partial J}{\partial f} \frac{\partial f}{\partial \theta} = \bigl(\nabla_{\mathbf h} J \cdot \nabla_f \mathbf h \bigl) \nabla_\theta f \end{align}\]整理一下便可以得到本文结论(典型的动态规划递推公式)
\[\begin{align} \nabla_f J & = \nabla_{\mathbf h} J \cdot \nabla_f \mathbf h &,& \text{Residual}\\ \nabla_\theta J & = \nabla_f J \nabla_\theta f &,& \text{Gradience to parameter } \theta \end{align}\]可见损失函数\(J\)对参数\(\theta\)的梯度可以分为三个要件:
- \(\nabla_{\mathbf h} J\) 这个向量是损失函数对\(f\)所有直接后继节点的梯度
- \(\nabla_f \mathbf h\) 这个向量是\(f\)的所有直接后继节点对\(f\)本身的梯度
- \(\nabla_\theta f\) 这个数值就是\(f\)对参数\(\theta\)的梯度
注意前两个部分的点积组成了损失函数对\(f\)本身的梯度, 而这一梯度会在节点\(f\)的直接前驱节点的BP过程中使用到.
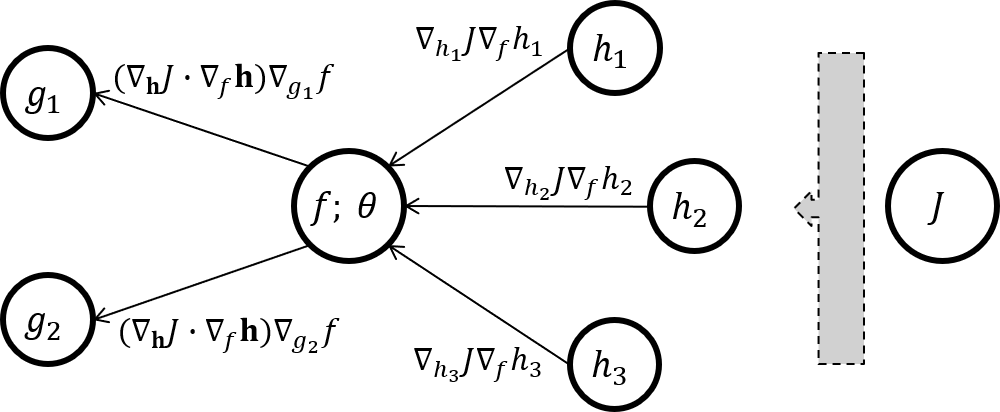
实际BP应用举例
在实际应用的时候, 也就是自定义一个神经网络的层的时候, 最需要注意的是, 只需要关心:
- 本层传递给后继层的输出是什么? (其shape必然仅与本层相关)
- 得到后继层反传来的残差后, 本层应该如何计算梯度并更新参数? (梯度的shape必然仅与本层参数的shape相关)
- 得到后继层反传来的残差后, 本层反传给前驱层的残差是什么? (其shape必然仅与本层的输入相关)
前馈全连接网络
如果前馈全连接网络的输入是\(\mathbf x_0\), 输出是\(\mathbf y\), 网络包含\(n+1\)层, 第\(i\)层的参数矩阵为\(\mathbf \Theta_i\), 则网络可以表示为
\[\begin{align} \mathbf x_1 & = f_0(\mathbf x_0, \mathbf \Theta_0)\\ \mathbf x_2 & = f_1(\mathbf x_1, \mathbf \Theta_1)\\ & \ldots\\ \mathbf x_n & = f_{n-1}(\mathbf x_{n-1}, \mathbf \Theta_{n - 1})\\ \mathbf{\hat y} & = f_n(\mathbf x_n, \mathbf \Theta_n)\\ \end{align}\]其中, 如果对于某一层\(i\), 其前驱, 本身, 后继层的节点个数分别为\(l, m, n\), 那么
\[f_i(\mathbf x_i, \mathbf \Theta_i) = \begin{cases} \mathbf \Theta_i \mathbf x_i, \quad \mathbf \Theta_i \in \mathbb{R}^{m \times l}, \mathbf x_i \in \mathbb{R}^l, & \quad \text{如果是连接层}\\ \max(0, \mathbf x_i), \quad \mathbf x_i \in \mathbb{R}^l, & \quad \text{如果是激活层且使用relu}\\ \end{cases}\]而目标为最小化损失函数
\[\min_{\Theta_0, \ldots, \Theta_n} J(\mathbf x_0, \mathbf y, \mathbf \Theta_0, \mathbf \Theta_1, \ldots, \mathbf \Theta_{n - 1}, \mathbf \Theta_n)\]为方便理解, 这里将\(\nabla_{f_i} J\)简写为\(\nabla_i\). 对第\(i\)层套用BP过程的结论
\[\begin{align} \nabla_i & = \phi(\nabla_{f_i} f_{i+1}, \nabla_{i+1}) = \phi(\nabla_{\mathbf x_{i+1}} f_{i+1}, \nabla_{i+1}) \quad \in \mathbb{R}^m\\ \nabla_{\mathbf \Theta_i} J & = \nabla_i \otimes \nabla_{\mathbf \Theta_i} f_i \quad \in \mathbb{R}^{m \times l} \end{align}\]其中
\[\begin{align} \phi (\mathbf A, \mathbf b) & = \begin{cases} \mathbf A^{\mathsf T} \mathbf b \text{(matrix-vector product)} & \quad \text{如果第}i+1\text{层是连接层}\\ \mathbf A \circ \mathbf b \text{(entry-wise product)} & \quad \text{如果第}i+1\text{层是激活层, 注意此时}l = m \text{且} \mathbf A \text{实际上是向量}\\ \end{cases}\\ \nabla_{\mathbf x_{i+1}} f_{i+1} & = \begin{cases} \mathbf \Theta_{i+1} \quad \in \mathbb{R}^{n \times m}, & \quad \text{如果第}i+1\text{层是连接层}\\ \max(0, \text{sgn}\bigl(\mathbf x_{i+1})\bigl) \quad \in \mathbb{R}^m, & \quad \text{如果第}i+1\text{层是激活层}\\ \end{cases}\\ \nabla_{\mathbf \Theta_i} f_i & = \begin{cases} \mathbf x_i \quad \in \mathbb{R}^l, & \quad \text{如果第}i\text{层是连接层}\\ 0, & \quad \text{如果第}i\text{层是激活层}\\ \end{cases} \end{align}\]练习题
- 卷积层的前向和后向过程分别是怎样的? (参考卷积神经网络概要)
- 池化层的呢?
- 各种Normalization层呢?
- 循环神经网络的呢?